Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
在百家樂這個具有高度策略性的賭博遊戲中，百家樂凱利公式被視為一個強大的工具，能夠幫助玩家在遊戲中取得更大的成功。這個公式以數學為基礎，旨在最大化玩家的長期收益率，使其能夠在激烈的賭場競爭中立於不敗之地。
深入了解和運用百家樂凱利公式，玩家可以精準計算下注金額，提高勝率並降低損失的風險。本文將從數學的角度出發，對百家樂凱利公式進行技巧性解析，讓玩家能夠掌握這一強大的工具，在百家樂的遊戲中取得更出色的表現。
一、凱利公式介紹
百家樂凱利公式是一種數學公式，用於計算在有固定賠率的賭博遊戲中，玩家應該下注的資金比例，這個公式的目標是最大化玩家的長期收益率。
這個公式由約翰·凱利（John Kelly）於1956年提出，起源於資訊理論，凱利公式適用於一系列機會性遊戲，其中玩家需要在不確定的情況下做出下注決定。
玩家可以透過百家樂凱利公式來計算下注金額，凱利公式的數學表達式如下：
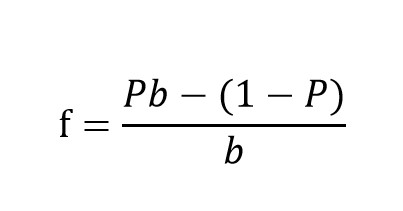
其中：
- f是應該下注的資金比例
- b是賭注的賠率，即贏得的金額與下注金額的比率
- p是成功的概率
- q是失敗的概率，即 1−p。
百家樂中，p和b 則根據賭注的種類和賭場提供的賠率來確定，取決於下注的種類和遊戲規則。bb 則根據賭注的種類和賭場提供的賠率來確定。
凱利公式的核心思想是找到一個下注比例，使得在長期內玩家的資金增長率最大化。然而，實際應用時，玩家可能會根據個人風險偏好和資金管理策略對計算結果進行調整。
凱利公式提供一個清楚的理論，幫助玩家更好地管理風險並提高長期收益。然而，需要注意的是，凱利公式假設玩家對概率和賭注賠率有完全的知識，並且不考慮其他因素，例如心理影響和資金限制。
因此，在實際應用中，玩家需要謹慎考慮公式給出的下注比例，並根據個人情況進行調整。
二、凱利公式理論與邏輯
凱利公式是一個基於數學和概率理論的模型，旨在幫助玩家計算最適合的下注金額，以最大化的方式提高長期收益，這個公式的核心邏輯是尋找一個下注比例，使得玩家在長期內資金增長率最大化。
這一公式的理論基礎來自資訊理論和概率論，資訊理論指出，當一個事件的機率已知時，該事件的資訊量越高，對該事件的預測就越準確，凱利公式利用這一原理，將下注金額與事件機率相關聯，確保玩家在長期內取得最佳的收益。
該公式的邏輯在於平衡風險和回報，通過計算出一個合適的下注比例，使玩家可以在潛在的風險下最大化其收益。然而，這代表凱利公式假設玩家對賭注的概率和賠率有完全的知識，並且不考慮其他因素，例如心理影響和資金限制。 凱利公式的理論基礎是建立在數學和概率論的基礎之上，邏輯在於通過適當的下注比例來最大化長期收益，並在風險與回報之間取得平衡。然而，在實際應用中，玩家需要謹慎考慮公式給出的下注比例，並根據個人情況進行調整。
三、凱利公式實戰運用於百家樂
1、凱利公式案實戰例舉
一個1賠2的簡單賭局，利用拋硬幣下注，假設賭注為1元，如果硬幣為正面，則淨贏2元，若為反面，則輸掉1元。再假設你現在的總資產為100元，每一次的押注都可投入任意金額，那麼，你會怎麼賭呢？
回答上面這個問題之前，我們先來簡單地分析一下，已知拋硬幣後正反面的概率都為50%，賠率是1賠2，那麼在這個賭局中，你只要有耐心地不斷去下注，再抛開一些不公平因素的干擾，你幾乎就能從中賺一筆。
因為拋硬幣次數越多，其正反面出現概率就越會穩定在50%，收益2倍，損失卻只是1倍，從數學上來講，那是穩賺不賠的賭局。
但實際情況卻可能會有偏差，如果你是激進主義者，你可能會想，要玩就玩一票大的！你可能會一次性把100元全押上，幸運的話，一次正面就可以獲得200元，那麼這又是一段值得炫耀的賭史。
反過來說，你如果輸了，就要把100元資產拱手獻給對方，你就一無所有了，那麼，這肯定就不是明策了。
但如果你是保守主義者，你可能會想，謹慎點，百分之一地慢慢玩，你每次只下注1元，正面贏2元，反面輸1元，玩了20把卻突然覺得，對方下注10元，一次就贏得20元，自己一次才贏2元，而10次才能贏得20元，感覺自己錯過了機會開始後悔！
那到底該以多少比例下注才能獲得最大收益呢？普通玩家會一臉茫然，但凱利公式卻能夠告訴我們一個正確答案：計算後每次下注比例為當時總資金的25%，這樣就能獲得最大收益。
2、什麼樣的情況才適合下賭呢？
凱利公式告訴我們，要通過選擇最佳的投注比例，才能長期獲得最高盈利。回到前面的引例中，硬幣抛出正、反面的概率都是50%，因此 p 和 q（分別為獲勝和失敗的概率）都是0.5。而賠率等於期望盈利除以可能虧損，即 2 ÷ 1，所以賠率就是2。也就是說，這個賭局次數越多，我們的收益就會越高。那麼，我們應該如何利用手中的資金來獲得最高收益呢？
要利用凱利公式來謹慎下注以獲得最高收益，首先需要計算最適合的下注比例。在這個例子中，因為正反面的概率都是50%，所以 p=0.5、q=0.5，賠率為 b=2。
接下來，我們可以使用凱利公式來計算最適合的下注比例 f∗：
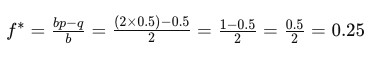
這代表根據凱利公式，最適合的下注比例為 0.25，即我們應該將資金的四分之一下注。舉例來說，如果我們手中有1000元的資金，根據凱利公式，我們應該下注 1000 的 0.25倍，即 250 元。
這樣，我們在長期內可以最大化我們的收益率，並將風險降到最低。然而，這也僅僅是理論上的最佳下注金額，實際操作中還需要考慮其他因素，如個人風險偏好和資金管理策略。
根據凱利公式計算後，我們得到了投注比例，即每次下注時都拿出當前手中資金的25%進行投注。 假設初始資金為100元，當硬幣為正面時，收益是投注金額的2倍；反之，則失去投注金額。在下表中，我們模擬計算了10次賭局的收益情況。
表1 25%投注下10次收益表：
| 賭局輪次 | 投資比例 | 投注金額 | 正反情況 | 本輪收益 | 資金結餘 |
| 1 | 25% | 25 | 正面 | +50 | 150 |
| 2 | 25% | 37.5 | 正面 | +75.00 | 225.00 |
| 3 | 25% | 56.25 | 正面 | +112.50 | 337.50 |
| 4 | 25% | 84.375 | 正面 | +168.75 | 506.25 |
| 5 | 25% | 126.56 | 正面 | +253.13 | 759.38 |
| 6 | 25% | 189.843 | 反面 | -189.84 | 569.531 |
| 7 | 25% | 142.39 | 反面 | -142.39 | 427.148 |
| 8 | 25% | 106.787 | 反面 | -106.78 | 320.361 |
| 9 | 25% | 80.090 | 反面 | -80.090 | 240.270 |
| 10 | 25% | 60.067 | 反面 | -60.067 | 180.203 |
25%投注下10次收益表
表2 投注下10次收益表：
| 賭局輪次 | 投注比例 | 投注金額 | 正反情況 | 本輪收益 | 資金結餘 |
| 1 | 25% | 25 | 正面 | +50 | 150 |
| 2 | 25% | 37.5 | 反面 | -37.5 | 112.5 |
| 3 | 25% | 28.13 | 正面 | +56.25 | 168.75 |
| 4 | 25% | 42.19 | 反面 | -42.19 | 126.56 |
| 5 | 25% | 31.64 | 正面 | +63.28 | 189.84 |
| 6 | 25% | 47.46 | 反面 | -47.46 | 142.38 |
| 7 | 25% | 35.60 | 正面 | +71.20 | 213.58 |
| 8 | 25% | 53.40 | 反面 | -53.40 | 160.18 |
| 9 | 25% | 40.05 | 正面 | +80.10 | 240.28 |
| 10 | 25% | 60.08 | 反面 | -60.08 | 180.20 |
投注下10次收益表
表1以先正後反的順序計算了收益，而表2則考慮了正反交替的情況下的收益結果。比較兩個表格，我們發現：它們的收益是相等的，也就是說硬幣正反面的出現順序對最終收益並沒有影響。
按照25%的投注比例進行下注，收益呈現出穩步增長的趨勢！然而，假設投注比例為100%，在10次投注中只要有一次反面，就會完全失去所有資金，面臨徹底出局，而每次只投注1元，即投注比例為1%時，雖然數學上的收益為105，但風險較小，收益卻不夠最大化！
